nate's site

CS + SE undergrad @ University of Western Ontario

Table of Contents

GitHub LinkedIn projects notes

Branching, Decoding and Addressing Modes

Branching

We’ve covered conditionals already, so let’s go into more depth

In total ARM instructions has 4 bits dedicated to 16 conditions

Untitled

Below is the meaning and encoding of each

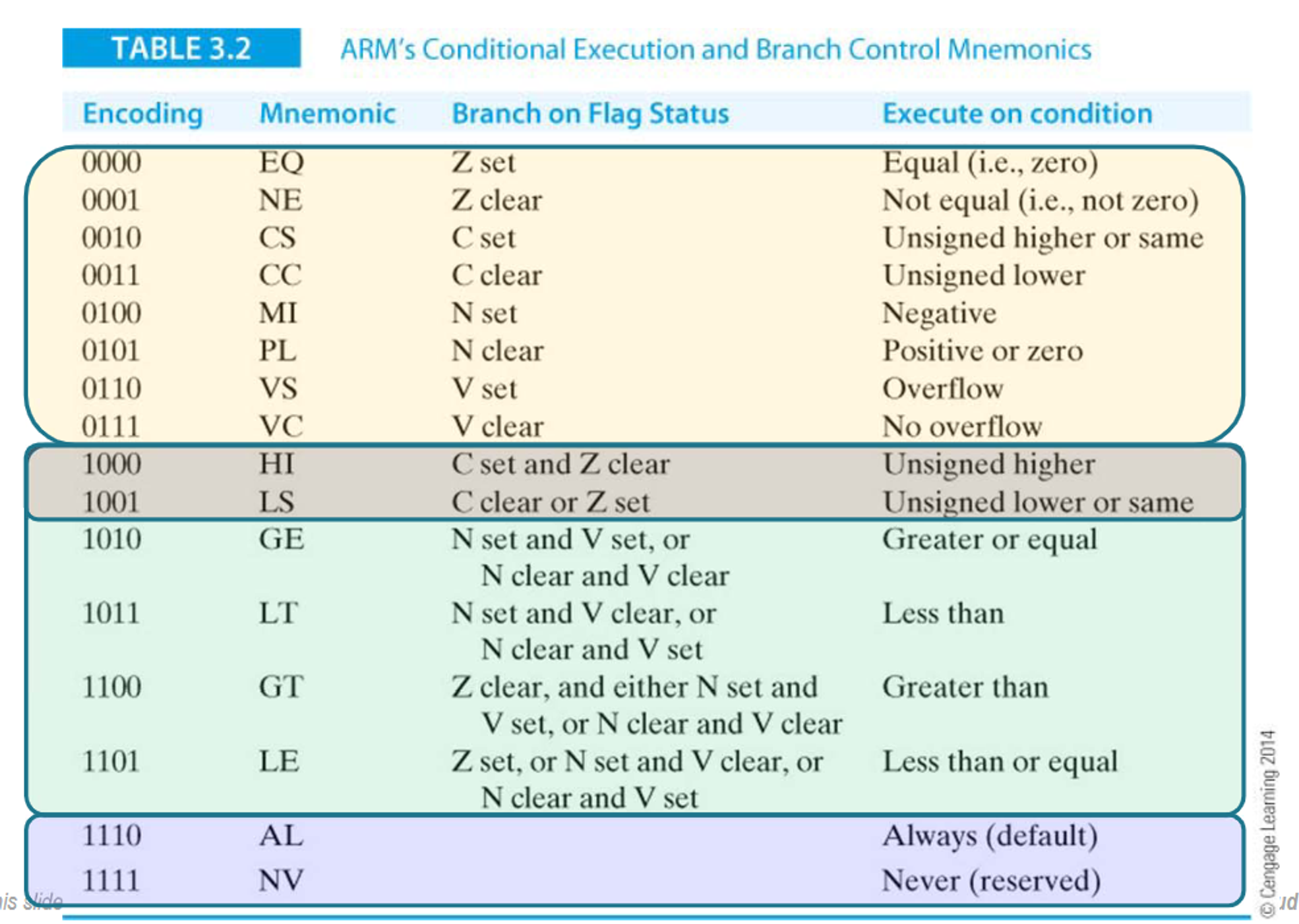
Untitled

Decoding

Branch instructions are encoded as such

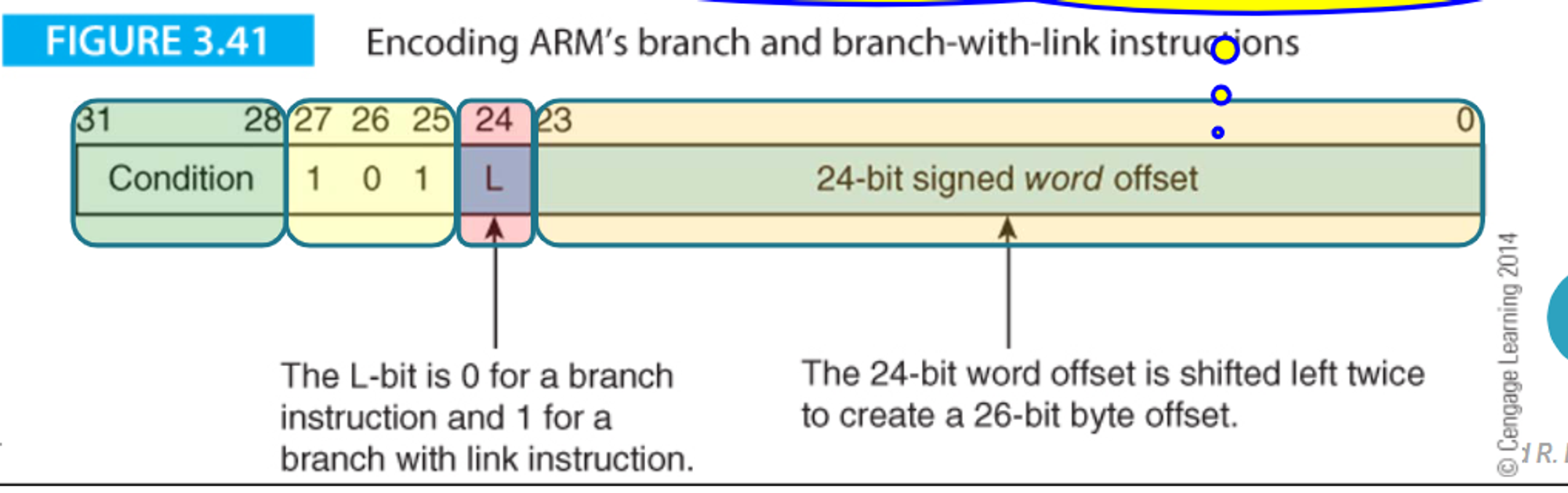
Untitled

For example, let’s say we want to decode the following instruction (signifying the end of a program)

loop B loop

First, since the branch has no condition, bits 28-31 will be 1110

Secondly, since there is no link, we need to set bit 24 to 0

Lastly, let’s look at the word offset; this offset signifies how many instructions we want to move forward by (or backwards with negative numbers)

Since we want to go back to the same instruction, we want to have an offset of 2

Translating this into two’s compliment, we get 1111 1111 1111 1111 1111 1110

Overall, our instruction is 1110 1010 1111 1111 1111 1111 1111 1110, or 0xEAFFFFFE in hex

For the reverse, let’s look at the instruction 0x1AFFFFFD

Translating into binary gives us 0001 1010 1111 1111 1111 1111 1111 1101, which we can then use for the rest of our encoding

Since bits 27-24 are 1010, we know this is a branching instruction with no link

Bits 31-28 are 0001, so we know the op-code is BNE

The offset is -3, which means we go 1 instruction backwards (taking into account pipelining)

So overall this is a BNE one step backwards, which would look something like this

marker ADDS r1,r1,r2
       BNE marker

Data Processing

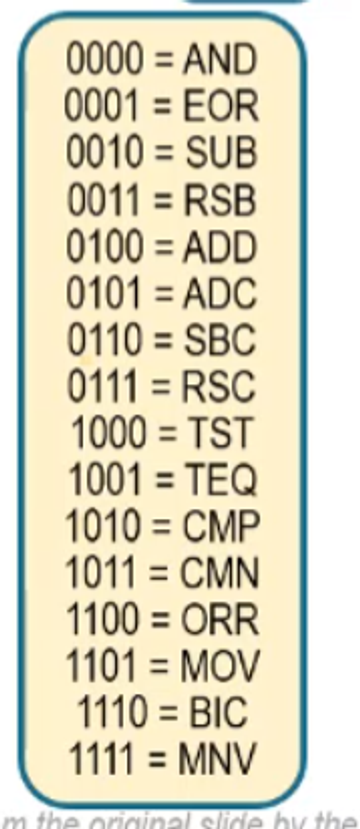
For data processing instructions, they go as such

Untitled

Untitled

For shift operations, we have some extra divisions

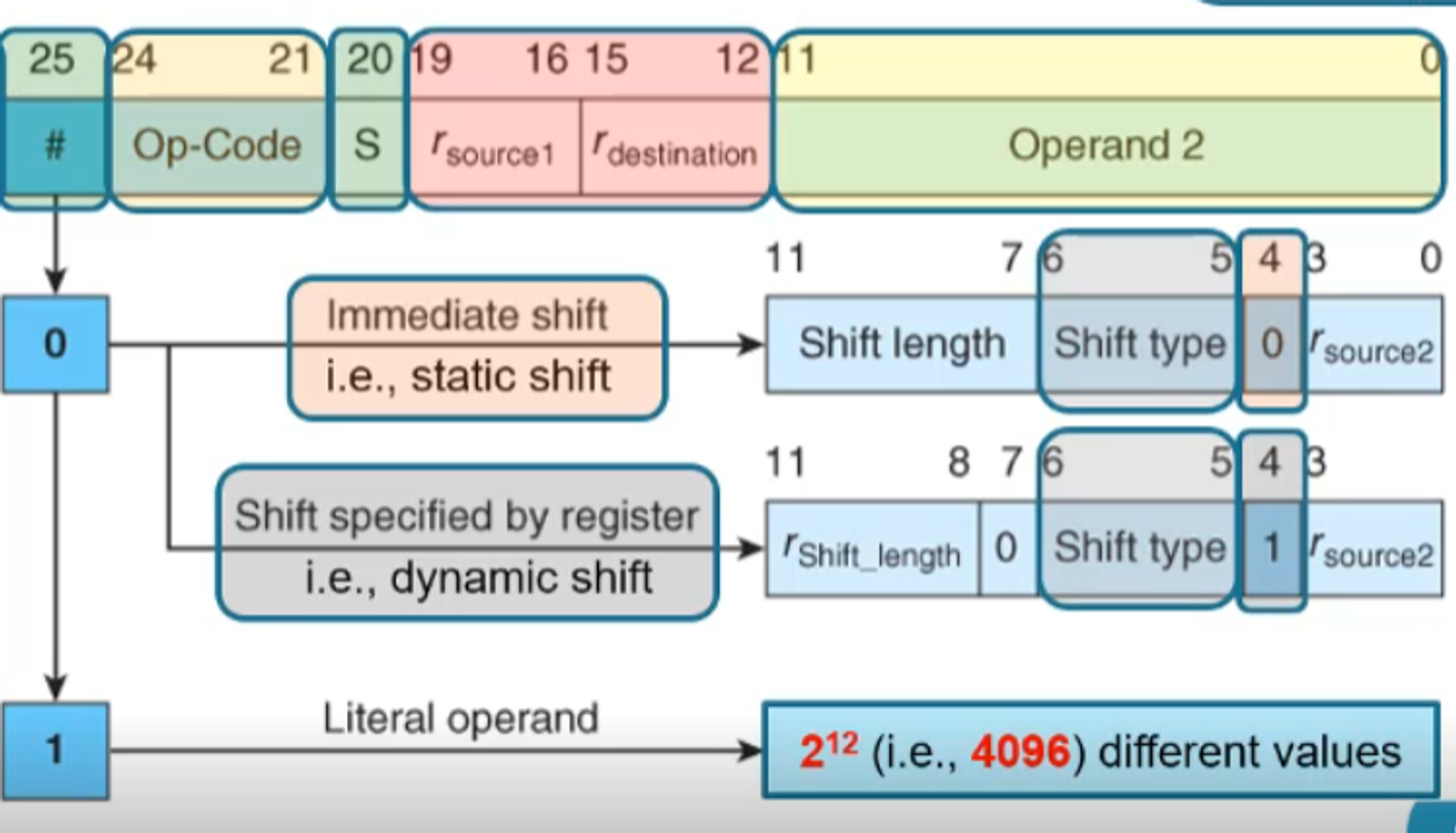
Untitled

The condition is still here because all instructions can be conditionally executed

For example, let’s encode the following instruction

ADD r0,r1,r2,LSR r3

Firstly, the condition is always, so bits 31-28 are 1110

Bit 25 indicates whether source 2 is a shift or a literal (it’s a shift, so we put 0)

Bits 24-21 are the op-code, for which ADD is 0100

Bit 20 indicates if there’s an S added to the op-code (there isn’t, so we put 0)

Bits 19-16 and 15-12 are the source 1 and destination registers, respectively, so we get 0001 0000

Bits 11-8 indicate the register that we will take for the shift length (it’s r3, so 0011), while bit 7 will be 0 since it’s a register-specified shift)

Bits 6-5 indicate the shift type (it’s a logical right, for which the code is 01)

Bit 4 will dictate if the shift is register-based (it is, so we put 1)

Finally, bits 3-0 indicate the second source (r2 = 0010)

Putting this all together, we get 1110 0000 1000 0001 0000 0011 0010 0011 (in hex, this is 0xE0A10332)

Comparisons

For comparison operations (ex. CMP, CMN, TST and TEQ), the destination is always r0 and S is always 1)

Let’s see this in action with an example

CMPGT r3,r5

In total, the instruction in binary is 1100 0001 0101 0011 0000 0000 0000 0101 (or 0xC1530005)

Moving

For MOV and MVN, source 1 is always 0

For example, let’s look at the following instruction

MOV PC,LR

Overall, the instruction is 1110 0001 1010 0000 1111 0000 0000 1110 (or 0xE1A0F00E in hex)

Handling Literals

Bits 11-0 can also be a literal, with bits 11-8 being an alignment representing half the desired rotations right and 7-0 being an 8-bit literal

For example, let’s look at the encoded operand 1110 1111 1111

So in total, the operand would be 1111 1111 0000, or 0xFF0 in hex

Addressing Modes

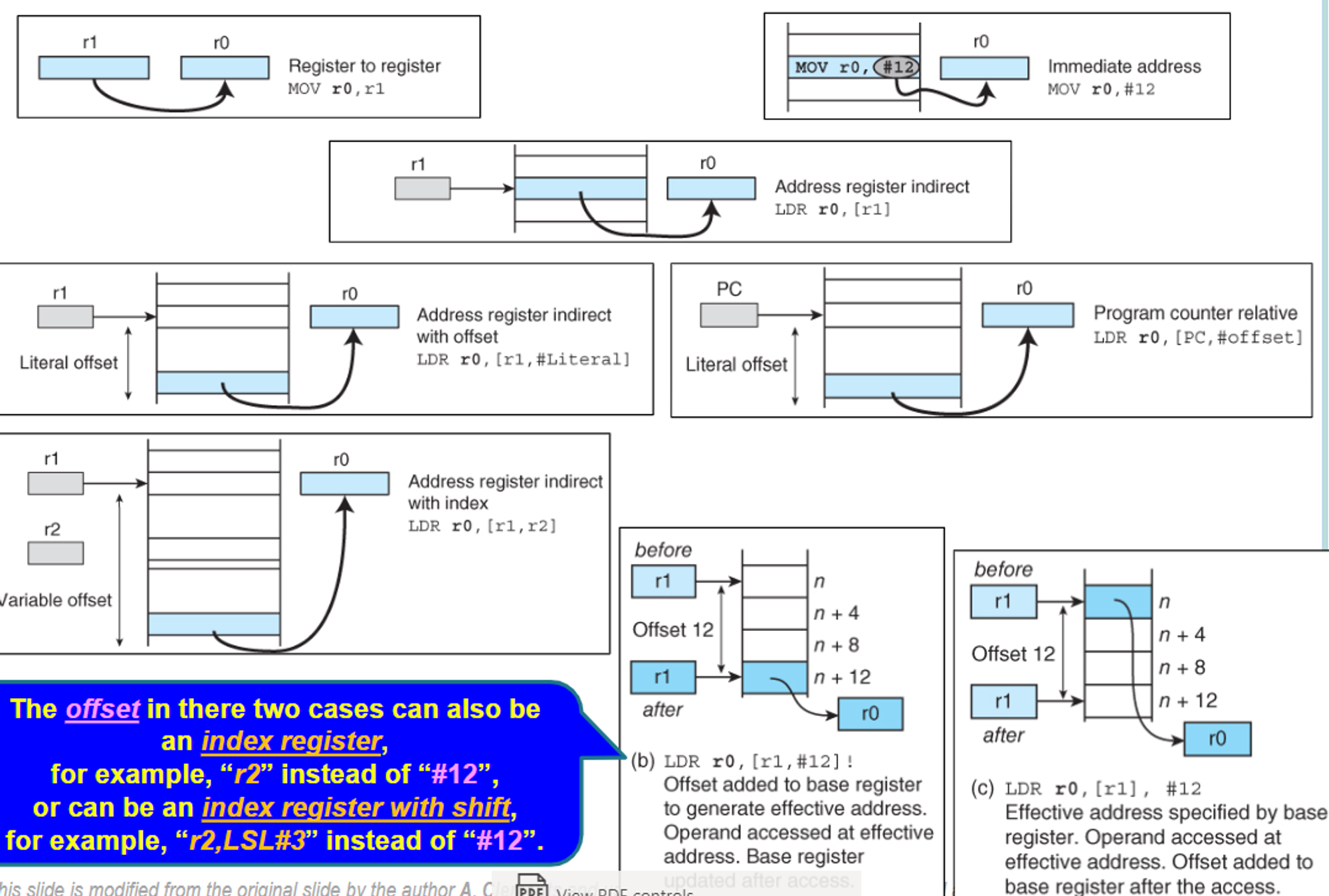
There are three addressing modes that we already know for getting info into registers:

  1. Literal (ex. [r0] ← [r1] + 2)
  2. Direct from memory, which isn’t supported by ARM (ex. [r0] ← [Mem])
  3. Register indirect, or loading a register with the content of a location in memory pointed to by another (ex. [r0] ← [[r1]] or LDR r0,[r1] in ARM assembly)

Since direct is impossible in ARM, register indirect with LDR and STR is the only way to actually access memory in ARM programs

The register with the address is indicated by square brackets, as seen in LDR r0,[r1]

We can use this for data structures such as arrays, which makes it vital for ARM programs

But how do we go backwards/forwards in an array like this? What we can do is subtract/add the register by 4 (i.e. one word), respectively

We can also do these types of offsets inside the brackets itself, like in the case of LDR r0,[r1,#4], which grabs the element one location ahead of what’s pointed to by r1

We can see this in action with the following program

Untitled

Just like other registers, we can use the program counter (r15) as a pointer register as well

We can also set dynamic offsets as well, such as in LDR r0,[r1,r2]

Something else useful we can do is automatically update the pointer itself, either by updating and then using (++r0) or using and then updating (r0++)

To summerize:

Untitled

LDR/STR and Stacks

LDR/STR

So far, we’ve covered how to encode every instruction except for LDR and STR

The basic format goes at so

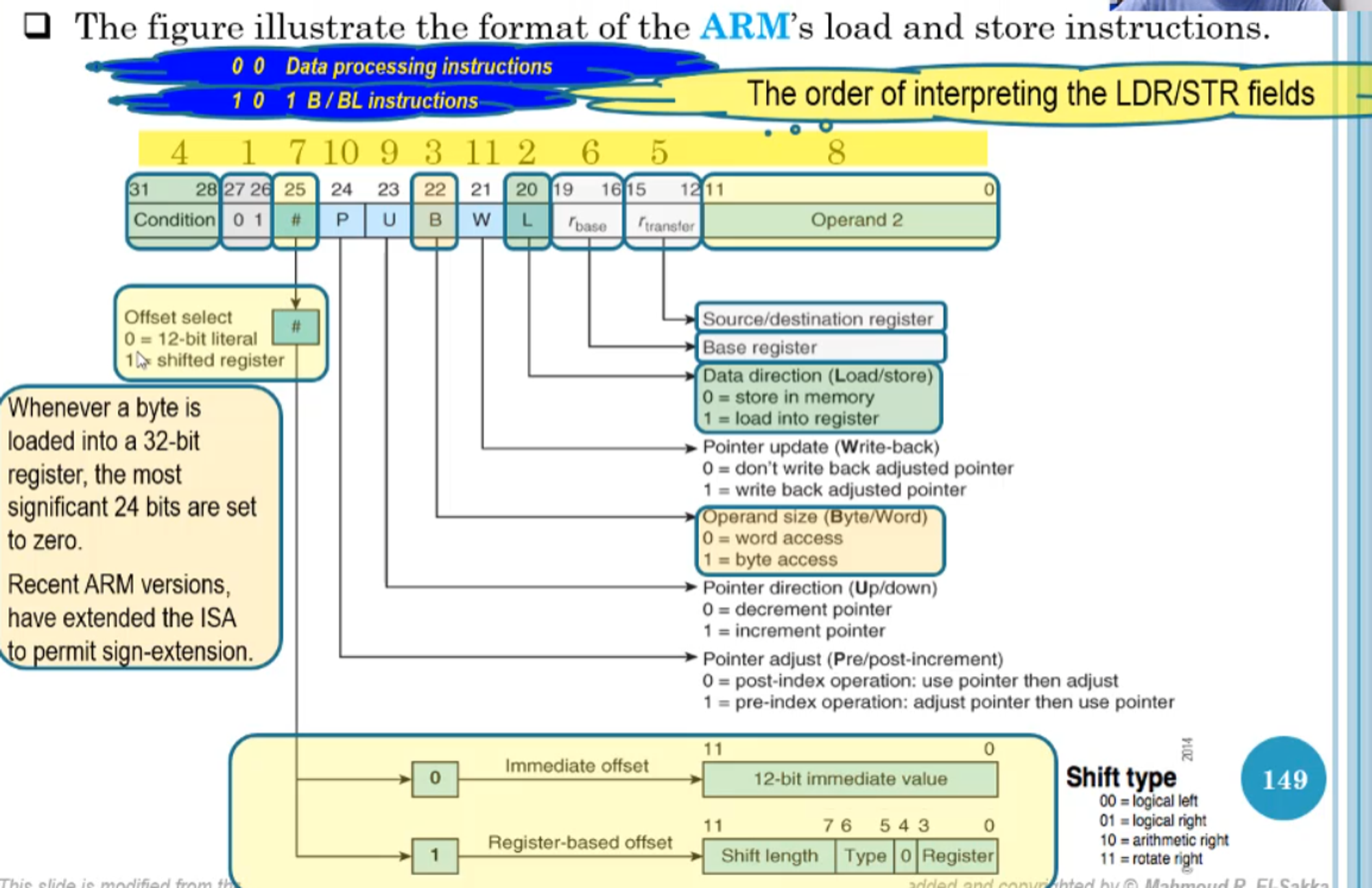
Untitled

As an example, let’s try to encode 0x57224106

Compiling all this together, we get the following

STRPL r4,[r2,-r6,LSL#2]!

For an encoding example, let’s look at the following instruction

STRGT r1,[r2,#-0xFFF]

Overall, we get 1100 0101 0000 0010 0001 1111 1111 1111 (or 0xC5021FFF in hex)

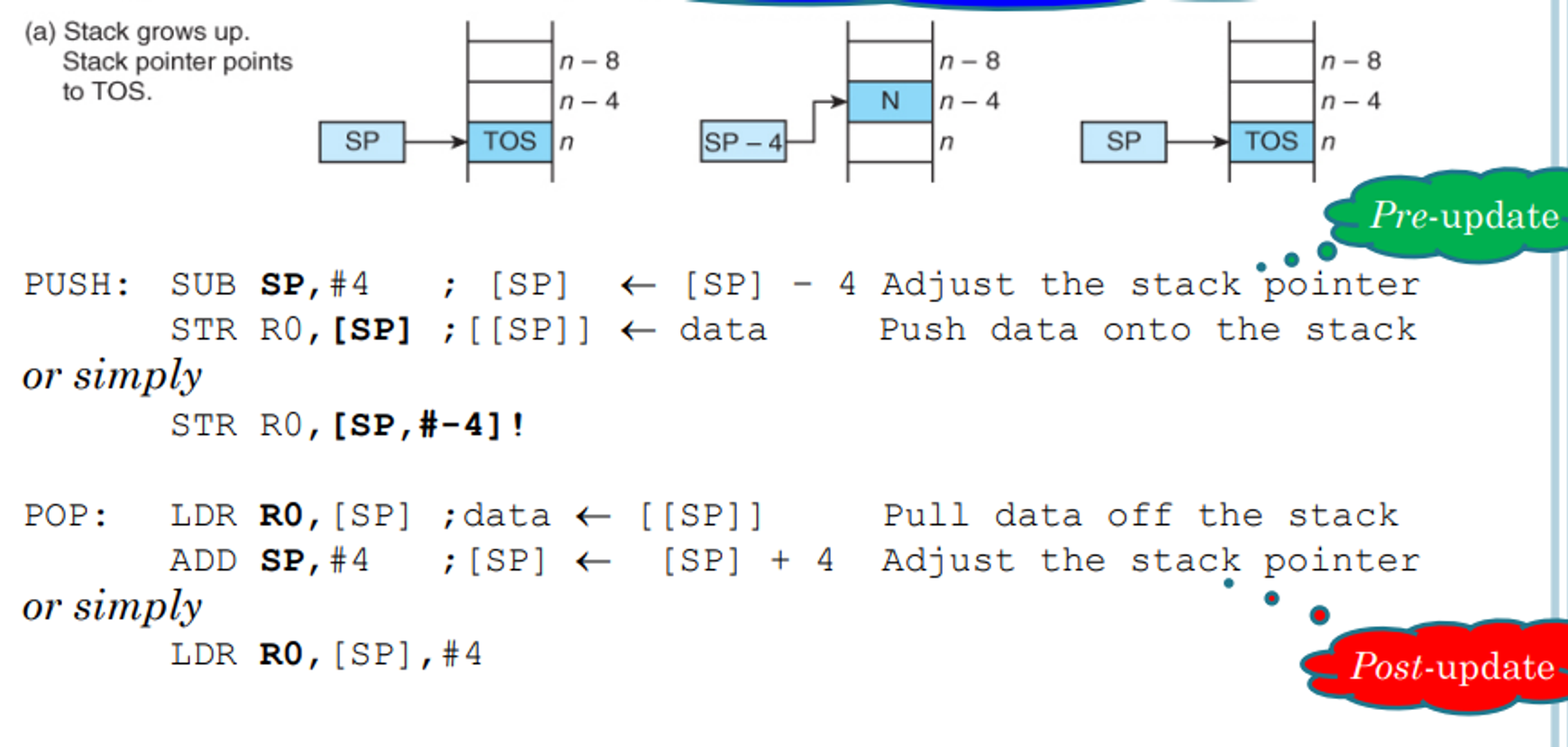
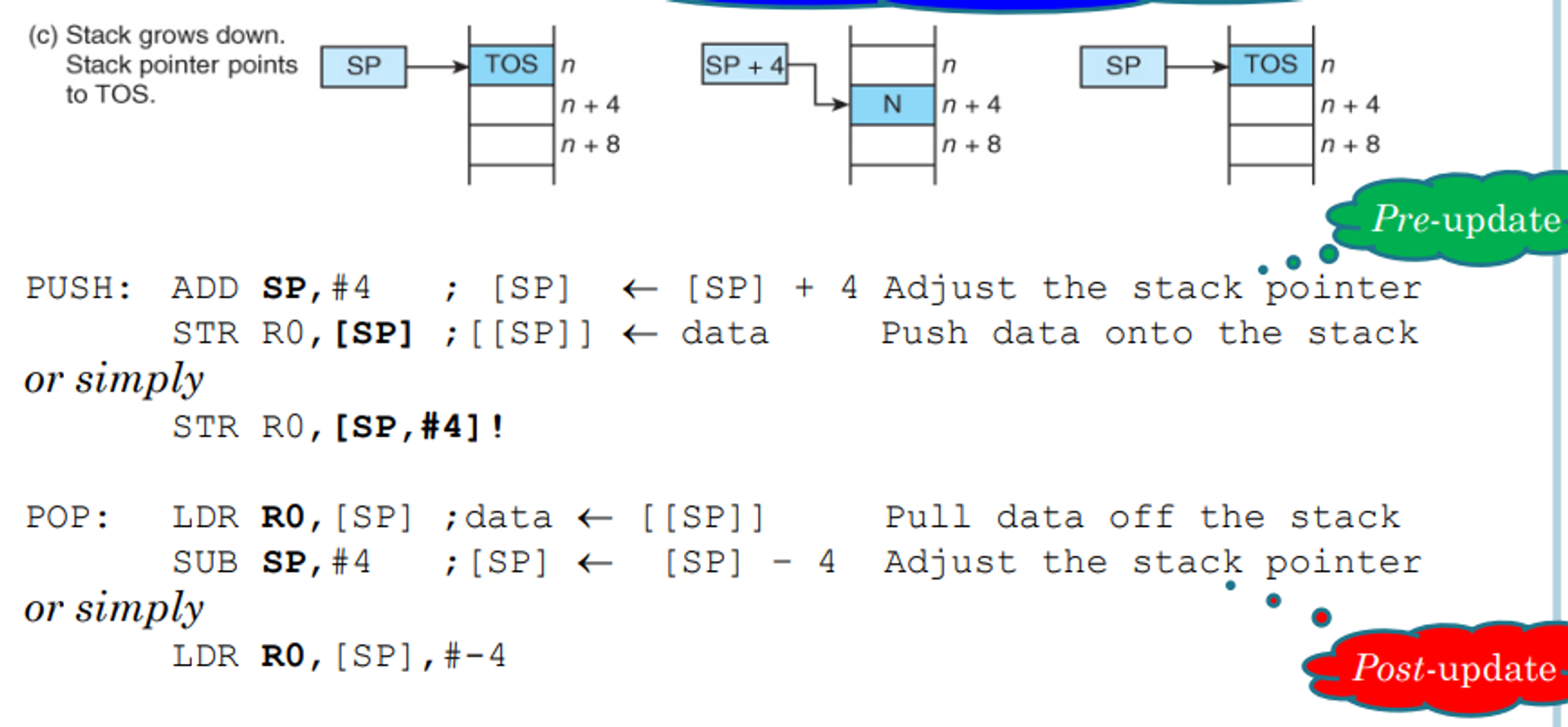
Stacks

Knowing these load and store instructions, we can not only implement arrays but stacks as well

As a refresher, stacks are a last in first out (LIFO) data structure in which items enter at one end and leave from the same end in reverse order

This type of data structure requires something called a stack pointer, which keeps track of the top of the stack and updates according to changes (moving forward on a push and backward on a pop)

There are four ways of forming a stack

  1. Growing up and pointing to the top of the stack (TOS)

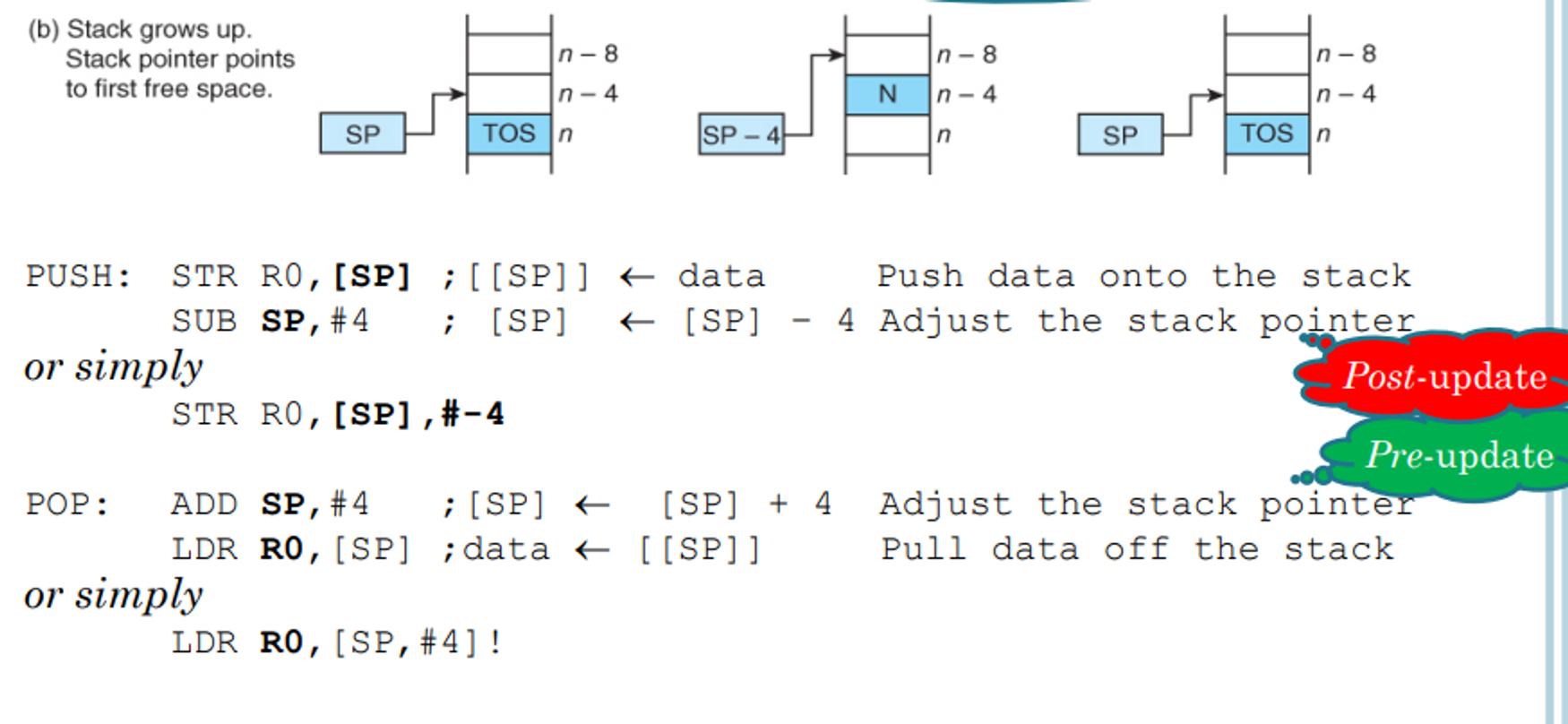
    Untitled

  2. Growing up and pointing one word above the TOS

    Untitled

  3. Growing down and pointing to the TOS

    Untitled

  4. Growing down and pointing one word below TOS

    Untitled

Block Moves and Subroutines

Block Moves

The last instructions we will cover are the block move instructions, LDM and STM

Assume we want to load a set of consecutive words from memory

Normally, we would have to add each word separately like so

Untitled

But with block move, we can combine all 4 instructions into 1

To make this easier to understand, you can think of STM as pushing a group of register content to memory and LDM as popping values from memory and loading them into register

For example, assume you have instructions like this

ADR r0,DataToGo
STMIA r0!,{r1-r3,r5}

Starting at the address pointed to by r0, the STM instruction will load words in order into the register r1, r2, r3 and r5

Note that the ! is important since it tells the computer to update r0

The two letters beside STM will tell you how the pointer will update

Usually for a stack we will have to leave some amount of space, which we can do pretty easily using SPACE

LDR r1,=0x11111111
LDR r1,=0x22222222
LDR r1,=0x33333333
LDR r1,=0x55555555
ADR r0,Stack
STMIA r0!,{r1-r3,r5}
Loop B Loop
SPACE 20 ;on exams we will be given both spaces, which one to use is up to you
Stack SPACE 20 ;we make space for each word needed + one buffer word = 16 + 4 = 20

Since these block move instructions implement stacks, we have special addons to simulate each type of stack

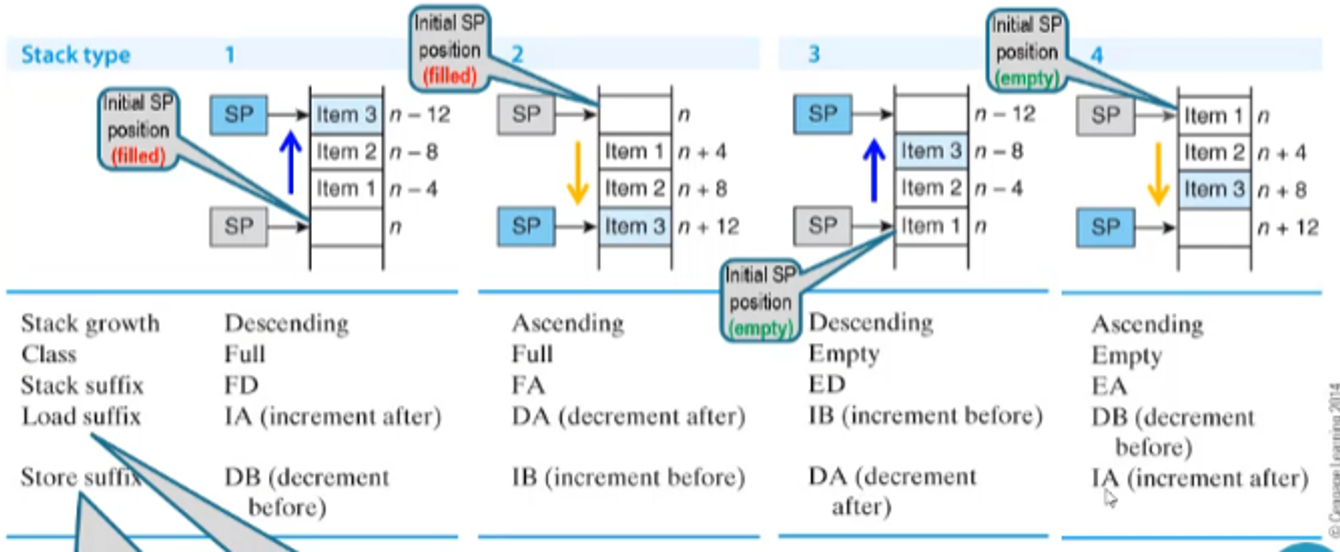
Untitled

Note that block move ≠ stack application, they just provide a means of moving memory content more efficiently

For example, if we want to move 256 words from one table to another in memory, we would have to load the memory into registers and load it back into memory at the specified location

Block move instructions can’t do all 256 words at the same time, but they can make the process much faster

ADR r0,Table1
ADR r1,Table2
MOV r2,#32
Loop LDMFD r0!,{r3-r10}
STMFD r1!,{r3-r10}
SUBS r2,r2,#1
BNE Loop

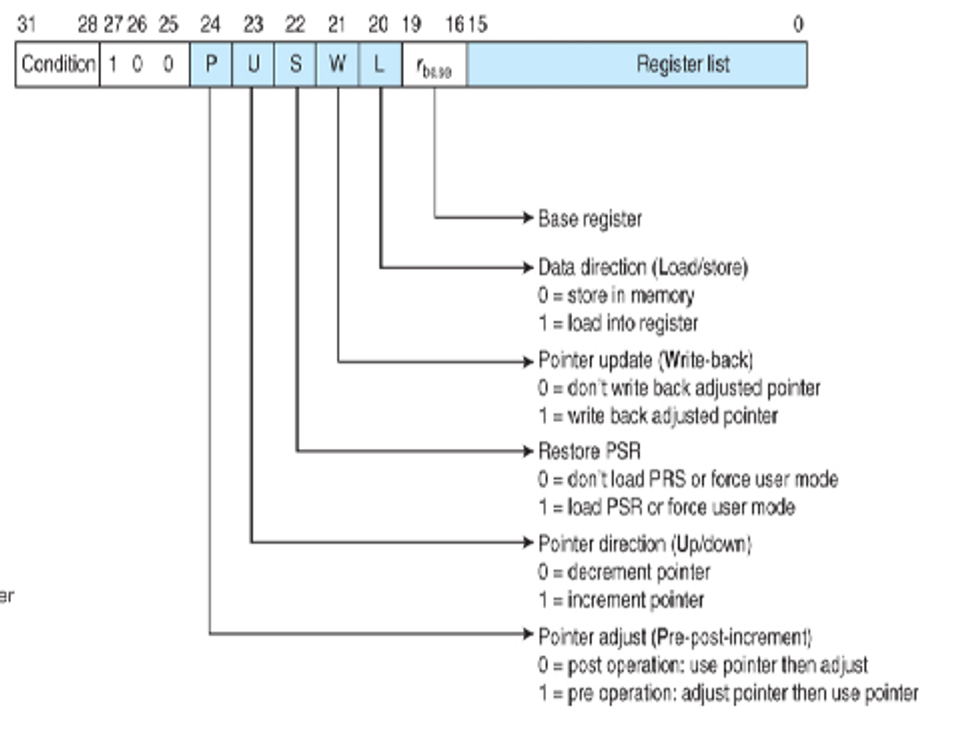
Encoding/Decoding

Encoding/decoding in block move works much like memory move, except the destination and second operand are replaced with a register list

The register list of each register, with its corresponding bit being 1 is the corresponding register is included in the range

For an example, let’s look at the following instruction

STMFD r13!,{r0-r4,r10}

Overall, the instruction is encoded as 1110 1001 0010 1101 0000 0100 0001 1111 (or 0xE92D041F in hex)

Untitled

For a decoding instruction, lets look at the instruction 0x08855555

Translating to binary, we get 0000 1000 1000 0101 0101 0101 0101 0101

Overall, this is the instruction that we get

STMEQIA r5,{r14,r12,r10,r8,r6,r4,r2}
;OR
STMEQEA r5,{r14,r12,r10,r8,r6,r4,r2}

Subroutines

In a program, oftentimes we need to execute some code multiple times throughout

Obviously we can just put in the code multiple times, but this gets messy and complicated fast

Instead of this, we can put the code into a subroutine

To understand subroutines and how they work, we need to understand its characteristics

  1. It can be called from anywhere in the program
  2. It should return to the instruction directly after the subroutine calling location

How this is done in ARM is that the processor will save the address of the next instruction in a safe place and then load the PC with the address of the first instruction in the subroutine

After the subroutine is complete, we have a return to subroutine instruction (RTS) which will cause the processor to return to the address immediately after the subroutine call

The flow control looks something like this

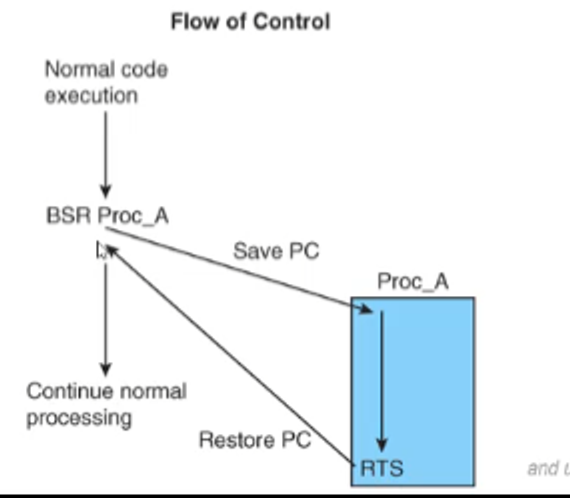
Untitled

CISC processors have fully automatic subroutine mechanisms, but in ARM it’s a bit more complicated

Subroutines in ARM

With BL

ARM’s branch with link instruction (BL) acts as a subroutine call, saving the return address in register r14

For example, let’s say we want to execute a subroutine Sub_A like so

BL Sub_A

At the end of Sub_A, we already have the return address in r14, so we can simply move r14 into r15

MOV r15,r14
;OR
MOV pc,lr

As a reminder of how these are encoded, we just take the old method and make bit 24 1

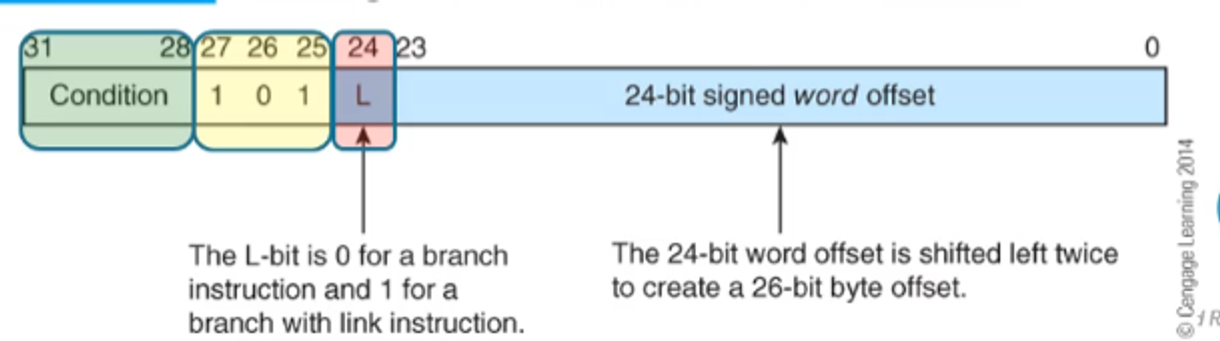
Untitled

With Stacks

We can also emulate a CISC processor and push the return address onto the stack before branching to the target address

Once the subroutine is finished, we can then pop the return address from the stack and copy it to the PC

For example, we can do something like this (assuming we have a Full Ascending stack)

...
...
...
STR r15,[r13,#-4]! ;pre-decrement the stack pointer AND
                   ;push the return address on the stack (DB)
B Target           ;NOT BL
...
...

Something we have to note is that usually the pipelining effect will have the PC be 8 bytes ahead of the current instruction, with the exceptions being STR and STM

STR and STM have a pipelining effect of +12, meaning the PC will be 3 instructions ahead instead of 2

How do we deal with this? Just load the top of the stack and add 4

...
...
LDR r12,[r13],#+4 ;get the PC and post-increment the stack pointer
                  ;r12 is just a general use register
SUB r15,r12,#4    ;fill the PC one instruction back from the return address

Nested Subroutines

The reason why knowing the stack method is important is that it’s the only way to implement nested subroutines

The way you have to handle nested routines is to save the link register in the stack before you call another subroutine

For example, take a look at the following program

Untitled

Since we call Fun_1 within Fun_2, we have to push the link register on the stack before we branch with link to Fun_1

From there, since Fun_1 is a leaf routine (a routine with no nested call inside of it), we just have to move the link register into the PC

At the end of Fun_2, we must then pop the original link register and load it into the PC (we don’t have to modify the link register value since pipelining is handled for us in branch with link)

Subroutines and Block Move

Assume that a program uses R1 to store a value, after which the program calls a function and R1 is used again to store a different value

This presents a problem because R1 will be overwritten, which will cause bugs

To avoid this, we should push all registers that will be used onto a stack at the beginning of a function and pop all of them into the same registers before returning from the function

For example:

Untitled