Parsing

The entire compilation process is encapsulated in the parser, so it’s very important to know how they work

Once the scanner grabs the token, it assembles them into a syntax tree and passes the tree through the parser, which is a language identifier

• A CFG, by contrast, is a language generator

As you may have learned from 3331, we can use the CYK algorithm to recognize languages, but this is a disastrously slow $O(n^3)$, but we can use $O(n)$ algorithms LL (left to right, leftmost derivation) and LR (left to right, rightmost derivation) to make the process faster

Class	Direction of scanning	Derivation discovered	Parse tree construction	Algorithm used
LL	left-to-right	left-most	top-down	predictive
LR	left-to-right	right-most	bottom-up	shift-reduce

In a top-down construction, we make predictions based on the next token, but in a bottom-up construction, we reduce the right-hand side

Left is top-down, right is bottom-up, both are using A, B, C;

With the bottom-up approach, we can get better grammars which can’t be parsed top down

Taking the same line, we can use bottom-up processing to get a parse tree like so

No matter which approach we use, we need to account for look-ahead, the number of characters we look ahead being defined by k

The higher the k, the more powerful the compiler gets, but the more complicated it gets

• Because of this, almost all real compilers use LL(1) or LR(1)
• We can use LR(0) to define the prefix property, which states that no valid string is a prefix of another valid string

Taking an example from last week, we can see that the choice between LL and LR is largely dependent on what we’re trying to do

LL(1) Grammar for Calculator Language

• Less intuitive: operands not on the same right-hand side
• Parsing is easier ($$ added to mark the end of the program)

program → stmt_list $$
stmt_list → stmt stmt_list | ε
stmt → id := expr | read id | write expr
expr → term term_tail
term_tail → add_op term term_tail | ε
term → factor fact_tail
fact_tail → mult_op fact fact_tail | ε
factor → ( expr ) | id | number
add_op → + | -
mult_op → * | /

Compare with LR Grammar:

expr → term | expr add_op term
term → factor | term mult_op factor
factor → id | number | -factor | (expr)
add_op → + | -
mult_op → * | /

Top-down Parsers

• By hand – recursive descent
• Table-driven

LL-Parsing

An approach we can take with LL-parsing is a recursive descent parser, where we have one subroutine for each nonterminal

Recursive Descent Parser

• One subroutine for each nonterminal

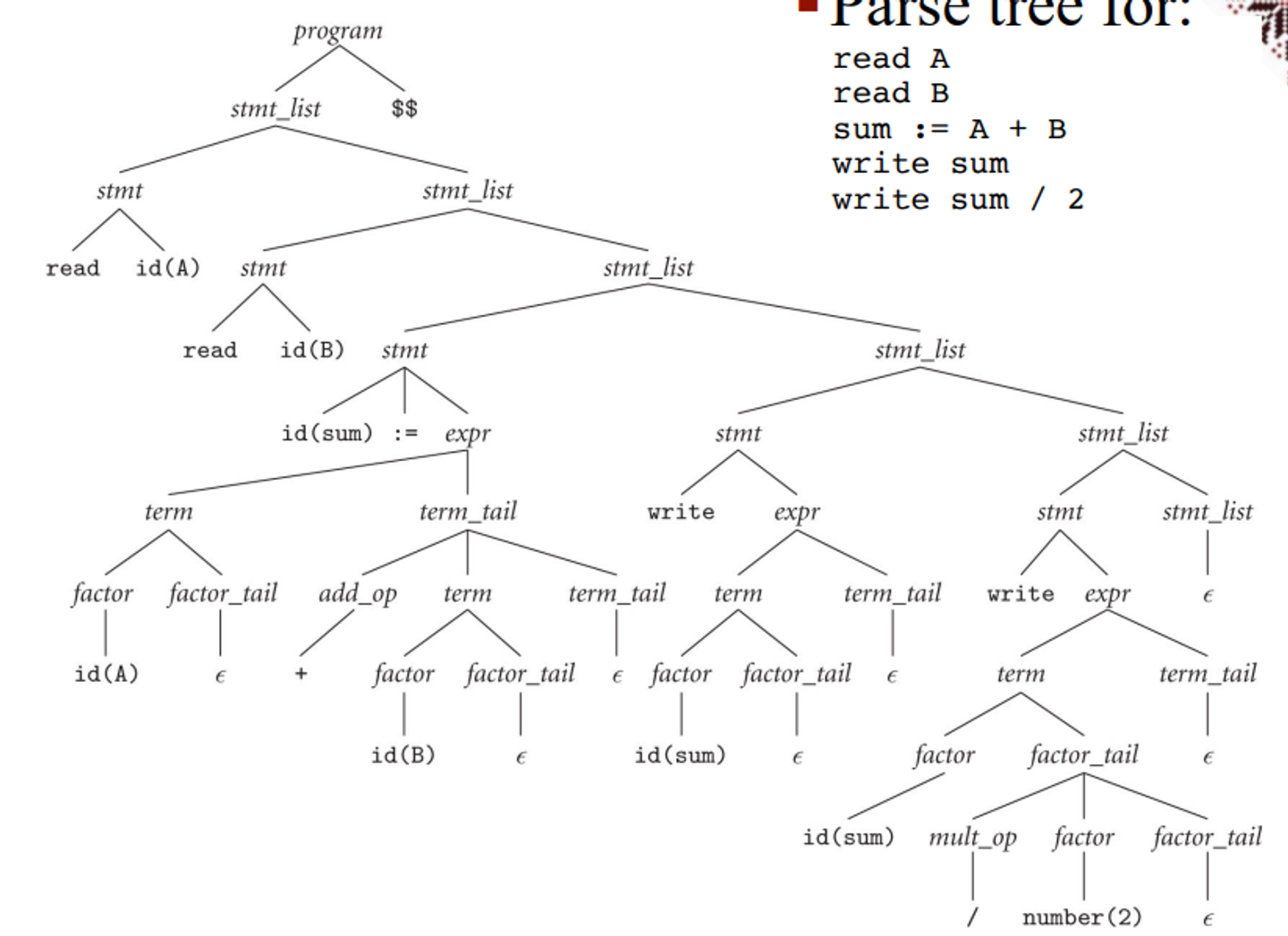
Example

read A
read B
sum := A + B
write sum
write sum / 2

procedure match(expected)
  if input_token = expected then
    consume_input_token()
  else
    parse_error

-- this is the start routine:
procedure program()
  case input_token of
    id, read, write, $$ :
      stmt_list()
      match($$)
    otherwise
      parse_error

procedure stmt_list()
  case input_token of
    id, read, write :
      stmt()
      stmt_list()
    $$ :
      skip  -- epsilon production
    otherwise
      parse_error

procedure stmt()
    case input_token of
        id : match(id); match(:=); expr()
        read : match(read); match(id)
        write : match(write); expr()
        otherwise parse_error

procedure expr()
    case input_token of
        id, number, ( : term(); term_tail()
        otherwise parse_error

procedure term_tail()
    case input_token of
        +, - : add_op(); term(); term_tail()
        ), id, read, write, $$ : skip -- epsilon production
        otherwise parse_error

procedure term()
    case input_token of
        id, number, ( : factor(); factor_tail()
        otherwise parse_error

procedure factor_tail()
    case input_token of
        *, / : mult_op(); factor(); factor_tail()
        +, -, ), id, read, write, $$ : skip -- epsilon production
        otherwise parse_error

procedure factor()
    case input_token of
        id : match(id)
        number : match(number)
        ( : match(()); expr(); match())
        otherwise parse_error

procedure add_op()
    case input_token of
        + : match(+)
        - : match(-)
        otherwise parse_error

procedure mult_op()
    case input_token of
        * : match(*)
        / : match(/)
        otherwise parse_error

When we read this out, we get the following parse tree

Another option is a table-driven approach, where we repeatedly look up actions in a 2D table based on the current leftmost non-terminal and the current input token

The actions we can take include

• Matching a terminal
• Predicting a production
• Announcing a syntax error

We run this with a pushdown automaton (PDA) with the stack containing the starting symbol

To build the table itself, we must build up a few functions

How to build the table:

• FIRST(α) – tokens that can start an α
• FOLLOW(A) – tokens that can come after an A

Definitions:

• EPS(α) ≡ if α ⇒* ε then true else false
• FIRST(α) ≡ { c | α ⇒* cβ }
• FOLLOW(A) ≡ { c | S ⇒* αAcβ }
• PREDICT(A → α) ≡ FIRST(α) ∪ if EPS(α) then FOLLOW(A) else ∅

Notes:

• If a token belongs to the predict set of more than one production with the same left-hand side, then the grammar is not LL(1).
• Compute: pass over the grammar until nothing changes.
• Algorithm and examples on the next slides.

Fortunately, we can calculate this with a simple algorithm

With our example grammar, it looks something like this

Common Problems

When creating a grammar that’s LL(1), we sometimes run into problems

The first problem is left-recursion, where $A \Rightarrow^+ A\alpha$ for some nonterminal $A$, the problem being that we can’t even parse it top-down

• Other types of recursion are fine

The way we solve this is by left-recursion elimination

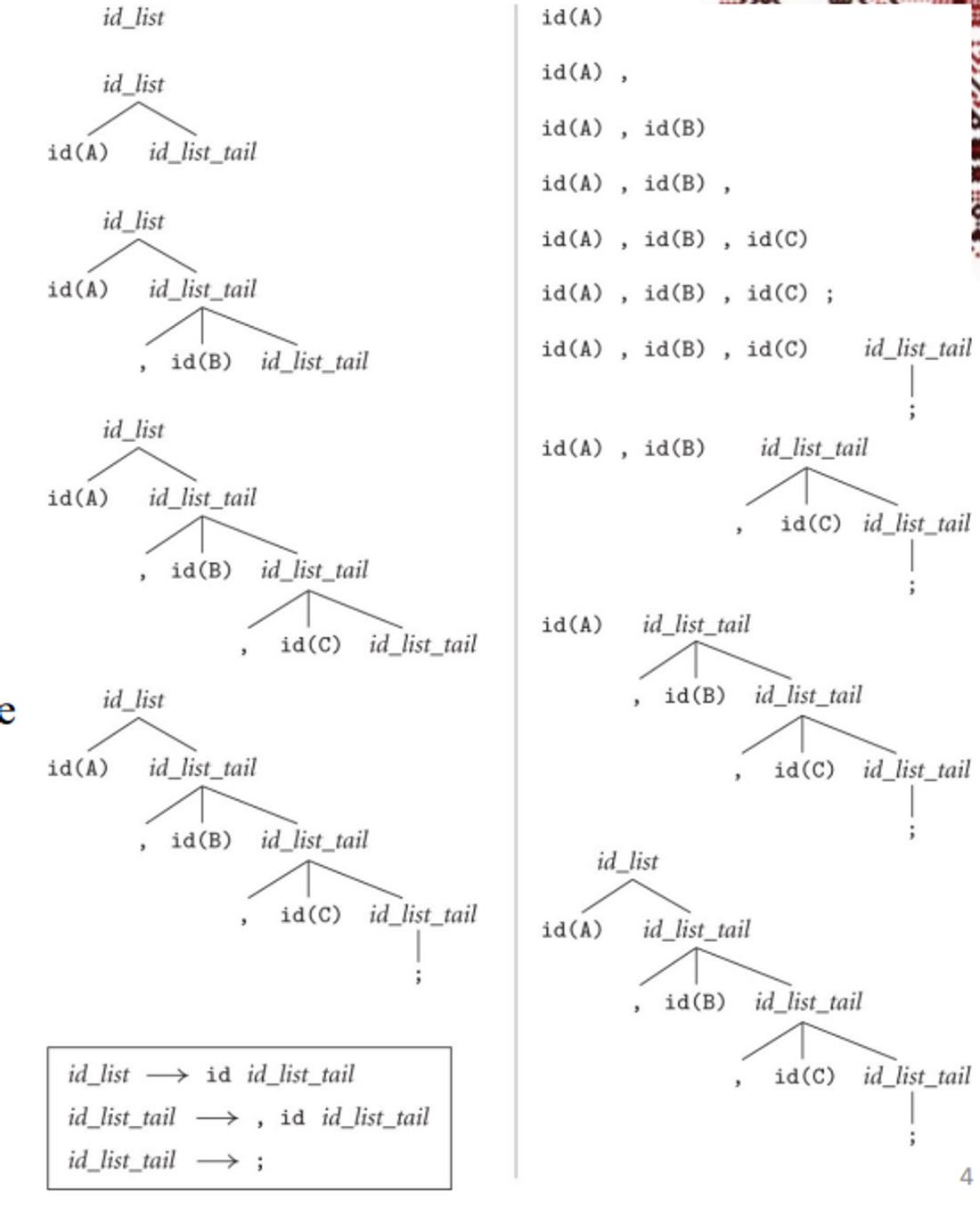
Example – cannot be parsed top-down

id_list → id_list_prefix ;
id_list_prefix → id_list_prefix , id
id_list_prefix → id

Solved by left-recursion elimination

id_list → id id_list_tail
id_list_tail → , id id_list_tail

There’s also the issue of common prefixes, but we must keep in mind that eliminating left-recursion and common prefixes doesn’t make it LL; there’s infinitely many languages that are not LL that can be automatically transformed without problems

Common Prefixes

Example

stmt → id := expr
stmt → id ( argument_list )

Solved by left-factoring

stmt → id stmt_list_tail
stmt_list_tail → := expr
stmt_list_tail → ( argument_list )

A real problem that DOES inhibit being LL is the dangling else problem

stmt → if cond then_clause else_clause | other_stmt
then_clause → then stmt
else_clause → else stmt | ε

if C₁ then if C₂ then S₁ else S₂

The issue with this is that it’s ambiguous, something that we can’t have when parsing in general

There’s two ways of solving this: the first is to make this unambiguous, which gives a good bottom-up grammar but will be impossible to do top-down

stmt → balanced_stmt | unbalanced_stmt
balanced_stmt → if cond then balanced_stmt else balanced_stmt
               | other_stmt
unbalanced_stmt → if cond then stmt
                 | if cond then balanced_stmt else unbalanced_stmt

The other way to handle this is an end marker, which adds an explicit ending to a statement

stmt → IF cond then_clause else_clause END | other_stmt
then_clause → THEN stmt_list
else_clause → ELSE stmt_list | ε

The issue with this is that we can have a bunch of ends bunched up, but this is a relatively easy fix

Problem with end markers: they tend to bunch up

if A = B then …
else if A = C then …
else if A = D then …
else if A = E then …
else …
end end end end

To avoid this: elsif

if A = B then …
elsif A = C then …
elsif A = D then …
elsif A = E then …
else …
end

You could also force an else for every if statement, but that’s a pain for any programmer using your language